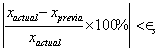Método de bisección
Método de bisección
El método de bisección se basa en el siguiente teorema de Cálculo:
Teorema del Valor Intermedio
Sea 
contínua en un intervalo 
y supongamos que 
. Entonces para cada 
tal que 
, existe un 
tal que 
. La misma conclusión se obtiene para el caso que 
.
Básicamente el Teorema del Valor Intermedio nos dice que toda función contínua en un intervalo cerrado, una vez que alcanzó ciertos valores en los extremos del intervalo, entonces debe alcanzar todos los valores intermedios.
En particular, si 
y 
tienen signos opuestos, entonces un valor intermedio es precisamente 
, y por lo tanto, el Teorema del Valor Intermedio nos asegura que debe existir 
tal que 
, es decir, debe haber por lo menos una raíz de 
en el intervalo 
.
El método de bisección sigue los siguientes pasos:
Sea 
contínua,
i) Encontrar valores iniciales 
, 
tales que 
y 
tienen signos opuestos, es decir,
|
|
|
ii) La primera aproximación a la raíz se toma igual al punto medio entre 
y 
:
|
|
|
iii) Evaluar 
. Forzosamente debemos caer en uno de los siguientes casos:
|
|
En este caso, tenemos que 
y 
tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo 
.
|
|
En este caso, tenemos que 
y 
tienen el mismo signo, y de aquí que 
y 
tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo 
.
|
|
En este caso se tiene que 
y por lo tanto ya localizamos la raíz.
El proceso se vuelve a repetir con el nuevo intervalo, hasta que:
|
|
|
es decir,
|
|
|
